Онлайн калькулятор для алгебраических вычислений: решайте уравнения, находите проценты, интегралы, пределы и многое другое. Наш удобный калькулятор поддерживает операции с дробями, матрицами, степенями, корнями, логарифмами, косинусами, синусами, арктангенсами и другими математическими функциями. Независимо от того, нужно ли вам найти решение уравнения, вычислить интеграл, или выполнить алгебраические операции, наш калькулятор всегда готов помочь. Используйте его онлайн и бесплатно – сделайте математику легче!
| Кнопки | Использование |
|---|---|
| 1 2 3 4 5 6 7 8 9 0 | Ввод цифр |
| + − × ÷ | Выполнение основных математических операций (сложение, вычитание, умножение, деление): 2 + 3 = 5 |
| = | Получение результата вычисления |
| C | Очистка экрана калькулятора |
| ← | Удаление последнего введённого символа: 1 2 3 4 ← 123 |
| ± | Изменение знака числа с положительного на отрицательный и наоборот: 3 ± −3 |
| ( ) | Ввод круглых скобок: ( 2 + 2 ) × 2 = 8 ПодробнееКруглые скобки используются для уточнения порядка выполнения операций в математических выражениях. Известно, что умножение и деление имеют более высокий приоритет, чем сложение и вычитание. Однако, когда нужно изменить порядок вычислений, круглые скобки вступают в игру и указывают, какую часть выражения нужно рассматривать сначала.
Допустим, у нас есть такое выражение: 2 * (3 + 4). Благодаря круглым скобкам мы знаем, что сначала нужно выполнить операцию внутри скобок, а затем умножить результат на 2. Если бы скобок не было, то мы бы сначала умножили 2 на 3, затем на 4, и только потом сложили результаты. Если мы хотим прояснить порядок действий, круглые скобки действительно помогают нам не запутаться. Они придают ясность математическим выражениям и упрощают их понимание. |
| . | Отделение дробной части в десятичной дроби: 0 . 1 + 0 . 2 = 0.3 Подробнее
Дробь – это математический объект, который представляет собой одно число, называемое числителем, деленное на другое число, называемое знаменателем. В общем виде дробь записывается как a/b, где a – числитель, b – знаменатель, и b ≠ 0 (потому что деление на ноль не определено в математике).
Дроби широко используются в математике и повседневной жизни. Они позволяют представлять части целого в форме числа, которое не обязательно является целым. Например, 1/2 представляет половину целого, а 3/4 – три четверти. Дроби могут быть положительными, отрицательными или нулевыми, но всегда остаются дробями. Они могут быть преобразованы в десятичные числа, а также можно выполнять различные операции, такие как сложение, вычитание, умножение и деление. |
| ÷ | Разделение числителя и знаменателя в обыкновенной дроби: 5 ÷ 8 − 1 ÷ 4 = 3/8 |
| 1/x | Вычисление обратного числа: 5 1/x = 0.2 Подробнее
Когда мы говорим о “вычислении обратного числа”, обычно имеем в виду нахождение числа, которое умноженное на исходное число даст нам 1. В математике для обратного числа часто используется термин “обратный элемент”.
Давай начнем с обратного числа в контексте обычных вещественных чисел. Для вещественных чисел (кроме 0) обратное число всегда существует. Например, обратное число для 2 – это 1/2, потому что 2 (1/2) = 1. То же самое касается и отрицательных чисел, например, обратное число для -3 – это -1/3, потому что (-3) (-1/3) = 1. Однако, когда мы говорим о вычислении обратного числа в модулярной арифметике, ситуация чуть сложнее. Например, в модулярной арифметике обратное число называется “обратный по модулю”, и оно существует только в случае, если исходное число и модуль взаимно простые (т.е. их наибольший общий делитель равен 1). |
| x2 x3 xy 10X | Возведение в степень: 3 x2 = 9 2 xy 4 = 16 5 10X = 100 000 Подробнее
Возведение в степень – это одна из основных операций в математике. Она используется для умножения числа на само себя определенное количество раз. Например, 2 возвести в степень 3 (обычно записывается как 2^3) означает умножить 2 на себя три раза: 2 * 2 * 2 = 8.
Математически запись a^n означает a, возведенное в степень n, где “a” – основание, а “n” – показатель степени. Если показатель степени равен 0, то любое число, кроме 0, возводится в нулевую степень, равной 1. То есть a^0 = 1. Помимо положительных степеней, существуют также отрицательные и дробные степени. |
| √x 3√x y√x | Нахождение корня из числа: 1 2 5 3√x = 5 1 6 y√x 4 = 2 Подробнее
Корень из числа – это число, которое, возведенное в заданную степень, дает исходное число. Например, если мы возьмем квадратный корень из числа 9, мы получим 3, потому что 3 возводим в квадрат дает 9.
Существует несколько видов корней, но наиболее распространенные из них – квадратный корень, кубический корень и общий корень. – Квадратный корень обозначается как √, например, √9 = 3. – Кубический корень записывается как 3√, например, 3√8 = 2, потому что 2 умноженное само на себя дважды даёт 8. – В общем случае n-ный корень обозначается как n√, где n – показатель корня. В математике корень из числа может быть как целым числом, так и дробным. Например, квадратный корень из 8 равен примерно 2.83, а не целому числу. |
| , | Разделение аргументов функции: log 9 , 3 = 2 |
| log | Вычисление логарифма: log 1 6 , 2 = 4 Подробнее
Логарифмы – это математическая функция, которая представляет собой обратную операцию возведения в степень. Они широко используются в различных областях науки, инженерии и математике из-за своей полезности при работе с большими числами и сложными математическими выражениями.
Логарифмы определяются относительно некоторой базы, обозначаемой как “a”. Обычно используются две основные базы: натуральный логарифм с базой “e” (приближенное значение 2,71828) и десятичный логарифм с базой 10. Логарифм числа “x” по базе “a” обозначается как “logₐ(x)”. Главная свойство логарифмов состоит в том, что они преобразуют операцию умножения в операцию сложения и операцию возведения в степень в операцию умножения. |
| e | Ввод математической константы e: log 1 , e = 0 Подробнее
Математическая константа “e” – это одна из самых важных и фундаментальных числовых констант в математике. Она называется “натуральным числом” или “числом Эйлера” в честь швейцарского математика Леонарда Эйлера, который в XVIII веке внес важный вклад в изучение этой константы.
Значение “e” приближенно равно 2,71828, но оно является иррациональным числом и имеет бесконечное число десятичных знаков без периодической структуры. Оно было впервые введено в математику как предел последовательности (1 + 1/n)^n, где “n” стремится к бесконечности. Этот предел имеет множество важных математических и физических приложений. “e” играет критическую роль в различных областях математики, физики и инженерии. Оно является основой для натуральных логарифмов и экспоненциальных функций, которые встречаются повсеместно в научных и инженерных приложениях. Формула “e^(ix) = cos(x) + i*sin(x)”, известная как формула Эйлера, связывает “e” с тригонометрическими функциями и комплексными числами и является одной из самых важных формул в математике. |
Преимущества калькулятора
- Отображение математических формул
- Поддержка больших чисел
- Решение уравнений
Инструкция по работе
В этом руководстве содержатся информативные инструкции по эффективному использованию данного калькулятора.
Глава 1: Ввод с помощью мыши
Нажимайте кнопки для ввода математической формулы или уравнения, как на карманном калькуляторе.
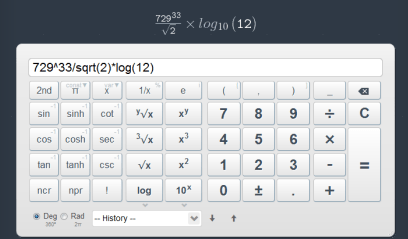
Глава 2: Ввод с клавиатуры
Если вы предпочитаете вводить математические формулы с клавиатуры, вы можете набирать их непосредственно в строке ввода. Нажатие кнопки ↵ запускает вычисление.

Глава 3: Функции
Чтобы вычислить функцию типа «синус» с аргументом 90, введите имя соответствующей функции, а затем аргумент 90 в круглых скобках. Пример: sin(90)
Виды калькуляторов
Калькуляторы – это устройства или программы, предназначенные для выполнения различных математических вычислений. Существует множество различных видов калькуляторов, каждый из которых предназначен для определенных задач. Вот некоторые из наиболее распространенных видов калькуляторов:
- Обычный калькулятор: это базовый калькулятор, который используется для выполнения основных арифметических операций, таких как сложение, вычитание, умножение и деление. Он может иметь как аппаратное, так и программное исполнение.
- Научный калькулятор: этот тип калькулятора предназначен для выполнения более сложных математических операций, таких как вычисление тригонометрических, логарифмических и экспоненциальных функций, а также для работы с числами в научной нотации.
- Финансовый калькулятор: финансовый калькулятор используется для решения финансовых задач, таких как расчет процентов, амортизации, чистой стоимости, внутренней нормы доходности и других финансовых показателей.
- Программируемый калькулятор: эти калькуляторы обычно используются программистами и инженерами для выполнения вычислений, связанных с программированием, и для создания и выполнения пользовательских программ.
- Графический калькулятор: графические калькуляторы позволяют строить и отображать графики функций и выполнять различные аналитические задачи, связанные с графикой и алгеброй.
- Инженерный калькулятор: эти калькуляторы предназначены для выполнения инженерных и технических вычислений, таких как преобразование единиц измерения, расчеты механики и электроники.
- Программное обеспечение калькулятора: кроме аппаратных калькуляторов, существует множество программных калькуляторов, доступных для установки на компьютеры и мобильные устройства. Они могут включать в себя различные функции в зависимости от своего назначения.
- Компьютерный калькулятор: встроенный в операционные системы компьютеров, этот калькулятор может выполнять разнообразные вычисления, включая программирование, конвертацию единиц измерения, стандартные арифметические операции и многое другое.
- Онлайн-калькуляторы: это калькуляторы, которые доступны через веб-браузеры и могут выполнять различные вычисления, включая финансовые, научные, графические и другие.
- Калькуляторы для специфических задач: существуют также специализированные калькуляторы для определенных профессиональных областей, такие как калькуляторы для бухгалтеров, инженеров, химиков, статистиков и др.
Это лишь некоторые из наиболее распространенных видов калькуляторов, и существует множество других калькуляторов, а также комбинированные варианты, предназначенные для выполнения разнообразных задач.
Применение калькуляторов в различных областях
- Финансы
В финансовой сфере калькуляторы используются для расчёта процентов, амортизации, инвестиций, ипотеки, и других финансовых операций. Программируемые калькуляторы часто используются для сложных финансовых моделей и статистических анализов. - Инженерия
В инженерии калькуляторы применяются для решения сложных математических задач, расчёта конструкций, электрических цепей, и других инженерных расчётов. Научные калькуляторы с функциями тригонометрии, логарифмов и дифференциального исчисления важны для инженеров. - Наука
В научных исследованиях калькуляторы используются для обработки данных, статистических расчётов, построения графиков и анализа результатов экспериментов. - Образование
Калькуляторы неотъемлемая часть учебного процесса. Они помогают студентам понять и применить математические концепции, проводить эксперименты, и решать задачи в классе и вне его. - Повседневная жизнь
В повседневной жизни калькуляторы используются для расчёта счетов, конвертации валют, подсчёта времени и дат, и других бытовых задач.
Виды вычислений, которые можно провести на математическом калькуляторе
На математическом калькуляторе можно провести огромное количество различных вычислений. Вот лишь некоторые из них:
Арифметические вычисления:
- Сложение: например, 2 + 2
- Вычитание: например, 5 – 3
- Умножение: например, 4 * 7
- Деление: например, 10 / 2
- Возведение в степень: например, 3^4 (3 в 4-ю степень)
Тригонометрические функции:
- Синус, косинус, тангенс
- Арксинус, арккосинус, арктангенс
- Гиперболические функции и их обратные
Логарифмы и экспоненты:
- Логарифмы: например, log(100) по основанию 10
- Экспоненты: например, exp(2) (число e в степени 2)
Работа с дробями и процентами:
- Перевод дробей в десятичные дроби
- Расчет процентов
Квадратные уравнения:
- Решение квадратных уравнений вида ax^2 + bx + c = 0
Конвертация единиц измерения:
- Пересчет валют
- Пересчет между различными системами измерения (например, длина, площадь, объем и т. д.)
Последовательности и ряды:
- Вычисление суммы арифметической или геометрической последовательностей
- Суммирование рядов
Статистика:
- Вычисление среднего, медианы, дисперсии и стандартного отклонения
- Расчет корреляции и регрессии
Матрицы:
- Умножение матриц
- Нахождение определителя
- Нахождение обратной матрицы
Другие функции:
- Факториал
- Абсолютное значение
- Округление чисел
Источники:
https://okcalc.com/ru/ 2023 OK Calc
https://web2.0calc.com/ 2006-2023 Andre Massow